Queue Simulation: Why Does the COVID-19 Pandemic Overwhelm Hospital Intensive Care Unit Bed Capacity

This article aims to demonstrate the application of Queueing Theory to model a service delivery system for capacity planning. A health care center administrator of a hypothetical 20-bed intensive care unit (ICU) plans to increase ICU bed capacity in response to a forecast of a daily average of ten new COVID-19 patients admitted from the emergency department or transferred from another facility. How many temporary beds will that be?

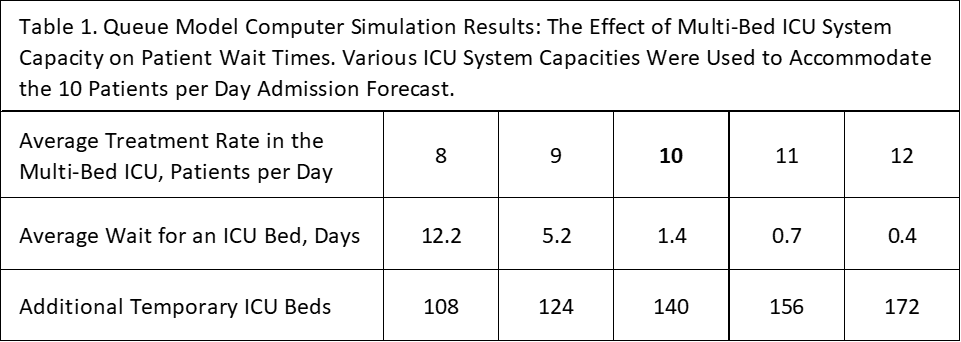
The simulation model illustrated above that embodies the queueing theory used simple formulas and built-in functions in Microsoft Excel. The model's computer formulation yields the length of time in days or fraction of a day an admitted patient waits in the queue for an ICU bed, the system’s performance measure. The service time of the ICU system expressed as the number of days a patient was on an ICU bed, were varied around the forecast of ten daily admissions and transfers.  Treatment rates of 8, 9, 10, 11, and 12 patients per day, completed the simulation campaign. Patient wait times were averaged from each simulation on a treatment rate and repeated over six simulations. Should hospital administration consider patient wait-times averaging 0.7 days as tolerable, the capacity of the ICU will have to raise to 11 patients per day or add 156 beds on top of the 20 it currently has.

To put this study from a real perspective, KPCNews.com, last July, reported 50,000 Covid-19 cases in Indiana as compiled by Regenstrief Institute. Of those cases, 7,800 required hospitalization in which 1,600 transferred to the state's ICU systems where patients stay for an average of 16 days. At the same time, there were 1,400 Covid-19 ICU beds in Indiana.

Theory of Queues

Queueing theory is a body of mathematical analyses that describe the behavior of service systems in terms of waiting lines or queues. A queueing model is a construct of customer arrival rate distribution, length of the wait, number and configuration of servers or ICU beds, and lastly, the distribution of service duration.  Information on one of these results from assumptions on other factors.  Queueing theory is generally considered a tool for managing service delivery operations and continuous improvement efforts to optimize resource deployment.

Queueing theory provides a robust management tool with applications in operational activities such as the fulfillment of online orders, intake to human services, call centers, bank tellers, vehicle fleet sizing, aircraft traffic control, and military defense.   

The Excel model clock begins during admission, continuous as the patient stays on an ICU bed, and ending at the time of discharge. As input, the model accepts assumptions on the average admissions to ICU per day and average days on an ICU bed per patient. Next, formula calculations proceed as follows: (a) sampling from Poisson distribution the time between the previous patient admitted to the current patient admission, (b) the patient waits in a queue if there are no vacant beds, (c) when a vacancy occurs, the treatment clock begins, (d) the length- of-treatment sampled from an exponential distribution is added to the time clock giving the time of discharge, and (e) the ICU bed is now available to the next patient at the queue.

This analytical tool benefits from the use of actual distributions of admission rates and length of stay in days in an ICU bed. For each simulation run, the model calculated the averaged waiting times of 900 patients from 1,000 patients tracked. The resulting wait times of the first 100 patients in a simulation run were removed from the calculation to reduce the initial effects inherent in computer simulations similar to this.

A free copy of the Excel model used in this study is available by request via email at Contact@mgmtlaboratory.com.

By Mgmtlaboratory.com staff.  2020