County Performance Comparisons: Chi-Square Testing for Similarity
Sans operating benchmarks, human service organizations cooperate by sharing each other’s operating ratios. Closer performance comparisons are enabled by finding and comparing ratios among similar agencies. The Chi-Square Test is another management tool that facilitates this effort. Conceptually, this analytical tool determines whether two frequency distributions, e.g. of discrete items or counts, are related or “similar” since both are samples of possible frequency distributions from a population of interest that is often immeasurable. For example, one may be interested in knowing whether the gender of the buyers of pronto pups is similar to the buyers of cheese curds at a state fair.

The administrator may seek measurements to ascertain that the agency’s operating performance in the delivery of high-quality services is best in class. One approach would be to compare operating ratios among services offered by similar counties. The following case study will demonstrate the use of statistical analysis to determine the demographic similarity of three counties regarding age.
At a Monday afternoon meeting with Lamar Smith, assistant administrator, and Sheila Marcello, planning manager, Ernie Gumban, Midwest County's administrator recounts last Friday's lunch with two of his peers from adjacent counties. Arlene Keranich is the administrator of Moon Lake County while Marcia Olson is the administrator of Renolds County. Moon County, with 61,180 residents, is the biggest of the three while Renolds County, with 10,390 residents, is the smallest, and Midwest County is in the middle with 32,860 residents. The three discussed how within their respective counties, operating ratios provided robust top-line performance measures and by sharing these measures with other counties, resulted in practical baselines for continuous improvement of service operations.
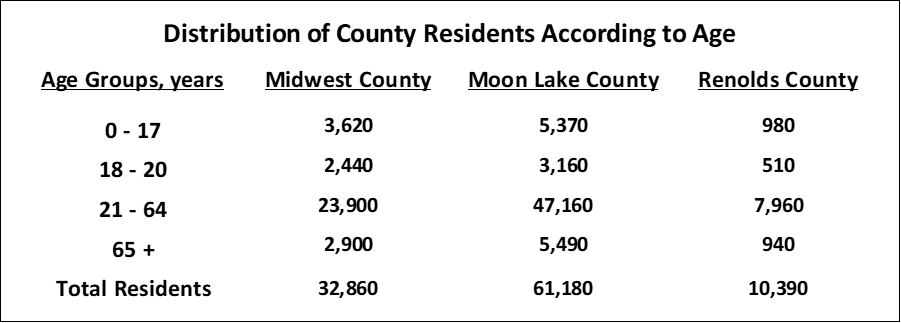
Ernie continued his recount of what transpired in the meeting. “Marcia was happy with the her workers' acceptance of using operating ratios in the workplace as Arlene and I are, but doubts still exist since Renolds County is small compared to us and to Moon Lake.” While pulling the demographic information sheet shown above from her briefcase, Sheila said, “The age distribution demographics from our planning system can be compared, but visually size is the only obvious factor. What we need is a way to quantitatively show with a high level of certainty that these age distributions are similar.”
"We can use the chi-square test to show their statistical similarity” Lamar exclaimed as he opened an Excel spreadsheet on his laptop. He pulled the age distributions of Moon Lake and Renolds from the planning system, calculated the expected residents in each age range and used the spreadsheet's chi-square test function. “This should make Marcia happy and remove any doubt in her workers’ minds,” said Lamar, “the statistical test indicated that there’s a 12 percent confidence that these distributions are similar.” Following Lamar’s analysis, Sheila proceeded to compare Midwest to Moon Lake. “My testing shows an almost zero percent confidence that the age distributions of Midwest and Moon Lake are similar, a finding that should boost confidence in the use of operating ratios in Renolds County’s workplace,” stated Sheila.
“Moreover, shared operating ratios of similar counties have been only used as guides that let workers know they are operating in the realm of practicality,” added Ernie. Ernie thanked Sheila and Lamar as he proceeded to contact his peers in Renolds and Moon Lake.
Working with the Chi-Square Test in Microsoft Excel
Lamar pasted the age distributions of the number of residents on an Excel worksheet shaded with yellow in the illustration. He then calculated the age group totals and the county totals.

For each actual number of residents in the yellow shaded area, a corresponding expected number of residents is calculated and are in the pink shaded area above. To calculate expected residents and take the count of residents in the 0-17 age range of Moon Lake County as an example. Its county total of 61,180 is first multiplied by its group total of 8,990 and then divided by the total of 94,040. Corresponding to the actual 5,370 residents, the expected value from this calculation is 5,849 residents. All of the expected values in the pink shaded area with varying county and group totals divided by the same total of 94,040 residents.
Once the numbers in pink are all calculated, the p-statistic is calculated. Place a “=” in an empty cell to evoke the function, “fn” in the menu tabs on top of the spreadsheet. Click on it and in the statistics menu select “CHISQ.TEST.” Copy the actual numbers of residents in the yellow field and paste these on actual numbers area of the function. Perform the same task, but this time, copy the numbers in the pink field. This function will give a p-statistic that will range from 0.0 to 1.0. If the p-statistic is equal or greater than 0.05, a generally accepted critical value, the similarity is indicated, while if below 0.05, the similarity is not supported.
All statistical analysis involves either inference or hypothesis testing. The latter rely on a null hypothesis and its counterpart, alternative hypothesis. In chi-square testing, the null hypothesis states that the differences between actual values and corresponding expected values are zero. The CHISQ.TEST function calculates the chi-square statistic and converts this to a p-statistic. The null hypothesis is indicated when p is equal to 0.05 or greater and the alternative hypothesis holds, otherwise.
By Noel Jagolino, Management Consultant
Mgmtlaboratory.com Content Contributor 2019


